8760. Поиск в
глубину
Задан неориентированный граф. Запустите поиск в
глубину из заданной вершины v и
выведите номера вершин в порядке их первого посещения.
Вход. Первая строка содержит количество вершин n (n
≤ 100) и ребер m графа. Каждая
из следующих m строк содержит две
вершины a и b – неориентированное ребро графа. Последняя строка содержит
вершину v.
Выход. Запустите поиск в глубину из вершины v и выведите номера вершин в порядке их
первого посещения.
|
Пример входа 1 |
Пример выхода 1 |
|
3 3 1 2 2 3 1 3 2 |
2 1 3 |
|
|
|
|
Пример входа 2 |
Пример выхода 2 |
|
5 3 1 3 2 3 2 5 5 |
5 2 3 1 |
РЕШЕНИЕ
графы – поиск в глубину
Анализ алгоритма
Построим
матрицу смежности по списку ребер. Запустим поиск в глубину из заданной вершины
v. Каждый
раз когда будем входить в новую вершину, выводим ее номер.
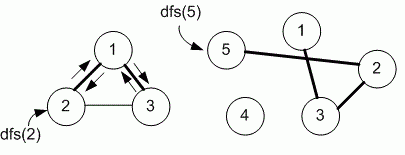
Решите задачу для следующих графов:

Реализация алгоритма – матрица смежности
Объявим
матрицу смежности g и массив used.
#define MAX 101
int g[MAX][MAX], used[MAX];
Функция dfs совершает поиск в глубину из вершины v.
void dfs(int v)
{
Выводим вершину v.
printf("%d ", v);
Отмечаем вершину v как пройденную.
used[v] = 1;
Перебираем вершины i, куда
можно двигаться из v. Передвижение из v в i возможно,
если:
· существует ребро (v, i),
то есть g[v][i] = 1;
· вершина i еще не пройдена
(used[i] = 0)
Если оба условия
верны, то продолжаем поиск в глубину из вершины i.
for (int i = 1; i <=
n; i++)
if ((g[v][i] == 1) && (used[i] == 0)) dfs(i);
}
Основная часть программы. Читаем количество вершин n и ребер m в графе.
scanf("%d %d", &n, &m);
Обнуляем массивы.
memset(g,
0, sizeof(g));
memset(used,
0, sizeof(used));
Читаем список ребер. Строим матрицу смежности.
for (i = 0; i < m; i++)
{
scanf("%d %d", &a, &b);
g[a][b] = g[b][a] = 1;
}
Читаем вершину v и запускаем из нее поиск в
глубину.
scanf("%d", &v);
dfs(v);
printf("\n");
Реализация
алгоритма – список смежности
Объявим список смежности g и массив used.
vector<vector<int> > g;
vector<int> used;
Функция dfs совершает поиск в глубину из вершины v.
void dfs(int v)
{
Отмечаем
вершину v как пройденную.
used[v] = 1;
Выводим
вершину v.
printf("%d ", v);
Массив g[v]
содержит список вершин,
смежных с v. Перебираем вершины to, в которые
можно пойти из v.
for (int to : g[v])
Рассматриваем
ребро (v, to). В вершину to можно пойти из v, если вершина
to еще не пройдена (used[to] = 0).
if (used[to] == 0) dfs(to);
}
Основная
часть программы. Читаем количество вершин n и ребер m в графе.
scanf("%d %d", &n, &m);
Устанавливаем
размер массивов g и used.
g.resize(n + 1);
used.resize(n + 1);
Читаем список
ребер. Строим список смежности.
for (int i = 0; i < m; i++)
{
scanf("%d %d", &a, &b);
g[a].push_back(b);
g[b].push_back(a);
}
Читаем
вершину v и запускаем из нее поиск в глубину.
scanf("%d", &v);
dfs(v);
printf("\n");
Java реализация – матрица смежности
import
java.util.*;
public class Main
{
static int g[][], used[];
static int n, m;
static void
dfs(int v)
{
System.out.printf(v + " ");
used[v] = 1;
for(int i = 1; i <= n; i++)
if (g[v][i] == 1 && used[i] == 0) dfs(i);
}
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
n = con.nextInt();
m = con.nextInt();
g = new int[n+1][n+1];
used = new int[n+1];
for (int i = 0; i < m; i++)
{
int a = con.nextInt();
int b = con.nextInt();
g[a][b] = g[b][a] = 1;
}
int v = con.nextInt();
dfs(v);
System.out.println();
}
}
Java реализация – array of ArrayList
import java.util.*;
public class Main
{
static ArrayList<Integer>[] g;
static int used[];
static int n, m;
static void dfs(int v)
{
System.out.print(v + " ");
used[v] = 1;
for(int to : g[v])
if (used[to] == 0) dfs(to);
}
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
n = con.nextInt();
m = con.nextInt();
g = new ArrayList[n+1]; // unchecked
used = new int[n+1];
for (int i = 1; i <= n; i++)
g[i] = new ArrayList<Integer>();
for (int i = 0; i < m; i++)
{
int a = con.nextInt();
int b = con.nextInt();
g[a].add(b);
g[b].add(a);
}
int v = con.nextInt();
dfs(v);
System.out.println();
con.close();
}
}
Java реализация – ArrayList of ArrayList
import
java.util.*;
public class Main
{
static ArrayList<ArrayList<Integer>> g;
static int used[];
static int n, m;
static void
dfs(int v)
{
System.out.printf(v + " ");
used[v] = 1;
for(int i = 0; i < g.get(v).size(); i++)
{
int to = g.get(v).get(i);
if (used[to] == 0) dfs(to);
}
}
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
n = con.nextInt();
m = con.nextInt();
g = new ArrayList<ArrayList<Integer>>();
used = new int[n+1];
for (int i = 0; i <= n; i++)
g.add(new ArrayList<Integer>());
for (int i = 0; i < m; i++)
{
int a = con.nextInt();
int b = con.nextInt();
g.get(a).add(b);
g.get(b).add(a);
}
int v = con.nextInt();
dfs(v);
System.out.println();
con.close();
}
}
Python реализация – список смежности
Функция dfs совершает поиск в глубину из вершины v.
def dfs(v):
Выводим
вершину v.
print(v, end = ' ')
Отмечаем
вершину v как пройденную.
used[v] = True
Список g[v] содержит
номера вершин, смежных с v. Перебираем вершины to, в
которые можно пойти из v. В вершину to можно
пойти из v, если вершина to еще не
пройдена (used[to] = 0).
for to in g[v]:
if not used[to]:
dfs(to)
Основная
часть программы. Читаем количество вершин n и ребер m в графе.
n, m = map(int, input().split())
Создадим список смежности g и список used.
g = [[] for _ in range(n+1)]
used = [False] * (n + 1)
Читаем список
ребер. Строим список смежности.
for _ in range(m):
a, b = map(int, input().split())
g[a].append(b)
g[b].append(a)
Читаем
вершину v и запускаем из нее поиск в глубину.
v = int(input())
dfs(v)